Mugichoko's blog

Mugichoko’s blog

しがない研究者のプログラミングを中心としたメモ書き．

検定ノート

Python お勉強 検定 ANOVA

使われる用語や用法が紛らわしく，最終的にはいつも詳しい先生にお尋ねして確認する事案，それが私にとっての検定．本投稿は個人的な整理のための記録です．間違っていたら是非とも指摘して下さい．

対応あり・なし (Paired / Unpaired)

  • あり：同じ時系列での前後の影響を測った（薬品投与の前後で血圧を測った）
  • なし：別のグループ・手法を使って影響を測った（薬品AとBを投与した後の血圧上昇度合を測った）

個人的に使いそうな検定

  • 反復測定分散分析 (Repeated measures ANOVA (within-subjects ANOVA))
    • 用いる状況
      • 同じ参加者が繰り返し「異なるタイミングで」もしくは「異なる条件を」施行する場合
      • 例：被験者の体温を毎週月曜日に一ヶ月間，部屋AとBで測る
    • 前提条件
      • 各観測は独立：同時に二つ観測して評価されるなどしていない
      • 正規性 (Normality)：正規分布に従う観測
      • 球面性 (Sphericity)：関連する群の全組み合わせ間の相違の分散が均等
      • 全条件が満たさた→反復測定分散分析を実行
      • 満たされなかった→フリードマン検定を実行
    • 事後検定 (Posthoc): Multiple pairwise comparison (t test ) with Benjamini'Hochberg FDR correction
    • 参考（その1）：https://www.reneshbedre.com/blog/repeated-measure-anova.html
    • 参考（その2）：https://www.statology.org/repeated-measures-anova-assumptions/
  • フリードマン検定 (Friedman test)
    • None-parametric検定の一種
    • 事後検定 (Posthoc): Mann-Whitney U / Wilcoxon rank sum test
      • use posthoc_wilcoxon!!

実装例

球面性と正規性の確認

import scikit_posthocs as sp
import pingouin as pg

# Shapiro-Wilk test
res_norm = pg.normality(data=df_tct, dv="TCT", group="Method")
print(res_norm, "\n")

# Mauchly’s test of sphericity
res_sph = pg.sphericity(data=df_tct, dv="TCT", subject="Participant", within="Method")
print(res_sph)

実行すると以下のような結果が得られる．この際，

  • 正規性：Normalが全てTrueか確認
  • 球面性：pvalが0.05より大きいか確認

以下の例ではどちらも確認できる，反復測定分散分析が実行できる．

反復測定分散分析

# ANOVA + the effect size
# https://www.marsja.se/repeated-measures-anova-in-r-and-python-afex-pingouin/
aov = pg.rm_anova(dv="TCT", within="Method", subject="Participant", data=df_err, detailed=True)
print(aov.round(2), "\n")

# Perform multiple pairwise comparisons (t test) and corrections (Benjamini/Hochberg FDR correction)
# https://www.reneshbedre.com/blog/repeated-measure-anova.html
post_hoc = pg.pairwise_ttests(dv="TCT", within="Method", subject="Participant", padjust="fdr_bh", data=df_err)
post_hoc

以下のように，群の全組み合わせの結果が表示される．p-corrの数値が0.05より小さければ有意差あり．

フリードマン検定

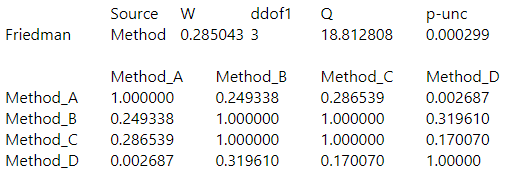
# Friedman test
res_f = pg.friedman(data=df_tlx, dv="TCT", within="Method", subject="Participant")
print(res_f, "\n")

# Mann-Whitney U / Wilcoxon rank sum test
res_w = sp.posthoc_mannwhitney(df_tlx, val_col="TCT", group_col="Method", p_adjust="bonferroni")
res_w

以下のように，群の全組み合わせの結果が表示される．数値が0.05より小さければ有意差あり．